Selections and Masked Operations

Dynamic sub setting of groups is achieved through masked operations that are executed conditionally depending on the current state of the individual group members. Conditions are expressed by means of boolean predicate functors. The masked collective map(), gather() and reduce() operations apply the specified functor only to those members for whom the specified predicate evaluates to true.

GroupOf<Member> group(...);
Result* resultByRank = new Result[group.size()];

group.map(predicate,...);
group.step(predicate,...);
group.gather(predicate,...);
Result r = group.reduce(predicate,...);

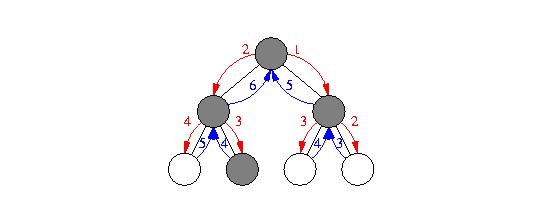
In the case of masked reductions (fig. [*]) the identity element of the reduction functor is filled in for all members that fail to match the specified predicate.

  

Figure: Masked reductions

Since the masked operations require visiting all members of the group they should only be applied if either the majority of members can be expected to match the predicate or the state of the members changes rapidly and unpredictably. Often recurring operations on the same subset should be implemented with selections instead.

Selections are indirect groups that refer to specific members of other groups. Unlike masked operations, selections allow dynamic sub-setting of groups with minimal communication overhead. When a selection is created, the membership is determined by a boolean predicate functor. Collective operations applied to the selection are in fact applied to the original group defined in the order of the selection's topology class.

CollectionOf<Any,BinTree> coll(...);
Selection<Any,List> sel(predicate, coll);

sel.map(...);
Result r = sel.reduce(...);

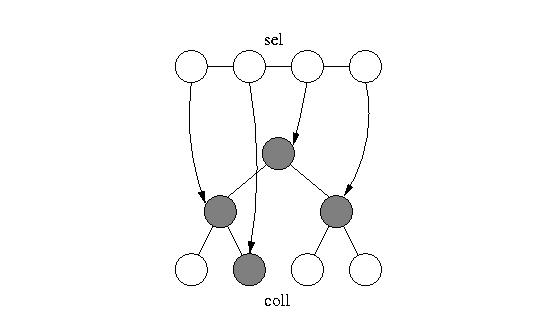
Note, that the topology of the selection and the original group may differ as shown in figure [*].

  

Figure: Selections

This allows us to create multiple selections with different topologies and we can choose those topologies that are most appropriate for the collective operations we are going to apply. When an application initially has a topology that does not support collective operations very well, we can easily create a complete selection with a tree topology that refers to all members of the original group and apply collective operations on the selection instead.